Liczba φ („phi”) to inaczej złota liczba. Johannes Kepler miał określić ją jednym z „klejnotów geometrii”. Wyraża stosunek nazywany boską proporcją lub złotym podziałem. Przypadkowo lub nie, pojawia się zazwyczaj tam, gdzie mamy do czynienia z poczuciem piękna, ładu i spokoju. W różnych dziedzinach sztuki, w życiu, w dziełach człowieka lub tworach natury. Zdaniem niektórych ma ona niezwykle silny związek z muzyką, znajduje bowiem swoje odzwierciedlenie w kształtowaniu formy i dramaturgii dzieł wielu wybitnych twórców. Czy rzeczywiście?
Złoty podział odnosi się do podziału odcinka na dwie części w taki sposób, aby stosunek długości dłuższej z nich do krótszej był taki sam, jak całego odcinka do części dłuższej. Wartość liczby phi wynosi φ = (1+√5)/2 = 1,618…, więc jest to liczba niewymierna. Złotym podziałem określa się jej sprzężenie, oznaczane dużą literą Phi: Փ = 0,618…. Badania nad nią rozpoczęli już pitagorejczycy, wskazując istnienie złotej proporcji nie tylko w figurach geometrycznych pochodnych od pięciokąta foremnego (m.in. w pentagramie), ale również w figurach przestrzennych (niektórych wielościanach foremnych). Fascynację tym zjawiskiem odnajdziemy na przykład w szkicach wielościanów foremnych Leonarda da Vinci.

(źródło: Mathematical Association of America)
Okazuje się, że złoty podział występuje często w budowlach architektonicznych, rzeźbach, obrazach, ale również w przyrodzie: ułożenie gałęzi, liści, łusek czy geometria kryształów. Liczba φ występuje m.in. w uważanych za doskonałe proporcjach ludzkiego ciała. Jest ona komponentem ideału piękna, ustalonego przez Greków w klasycznym kanonie. W latach trzydziestych XX wieku złote proporcje dostrzeżono w symetrycznych rysach twarzy sławnej ze swej szlachetnej urody tenisistki Miss Helen Wills.

W muzyce obecność złotej liczby kojarzona jest w pierwszej chwili z twórczością Béli Bartóka widzianą przez pryzmat koncepcji Ernő Lendvaïa. Zdaniem teoretyka, węgierski kompozytor podczas konstruowania formy oraz przy wyborze materiału dźwiękowego mógł się kierować zasadą złotego cięcia. Przykładowo w konstrukcji fugi w I części Muzyki na smyczki, perkusję i czelestę muzykolog wskazuje wielopoziomowy podział na kolejne segmenty, których stosunek długości równy jest liczbie Փ. Lendvaï podaje szereg utworów, w których ta idea jest mniej lub bardziej widoczna. Jego teoria, jakkolwiek odkrywcza jak na swoje czasy i stawiająca twórczość Bartóka w nowym świetle, spotkała się z krytyką w środowisku muzykologicznym. Wskazywano w niej pewne nieścisłości oraz – w niektórych przypadkach – niemożliwość słuchowej weryfikacji opisanych zjawisk. Taką opinię wyraża m.in. autor polskiej monografii Bartóka, Tadeusz A. Zieliński, odcinający się od koncepcji analitycznej Lendvaïa, którą uważa za czysto materiałową, spekulatywną i ignorującą doświadczenie słuchowe.
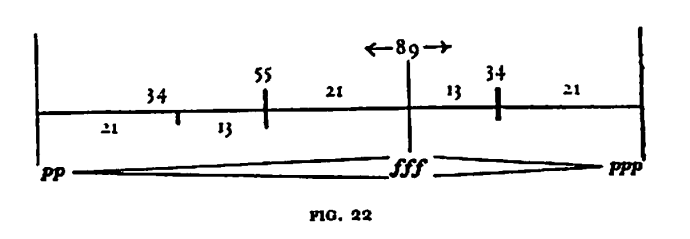
(źródło: Ernő Lendvaï, Béla Bartók. An analysis of his music, s. 28)
Trudno się jednak zgodzić z tą kategoryczną opinią Zielińskiego – wystarczy przytoczyć wspomnianą wcześniej fugę Bartóka. Nie można powiedzieć, że oparcie konstrukcji utworu na zasadzie złotej proporcji nie jest tutaj słuchowo nieuchwytne – wręcz przeciwnie, w części tej cała dramaturgia zbudowana jest w oparciu właśnie o tę zasadę: faktura i dynamika (kolejno wprowadzane głosy fugi) stopniowo narastają, aż do głównej kulminacji (złote cięcie), po której następuje fakturalne diminuendo. Lendvaï wylicza, że kulminacja przebiega dokładnie w punkcie złotej proporcji. Jednak, jak wskazuje Jonathan Kramer, wyliczenia te okazują się niedokładne, Lendvaï nie bierze pod uwagę obiektywnej długości trwania każdego taktu (ignoruje częste zmiany metrum, zmiany tempa), początkowy przedtakt uzupełnia do pełnego taktu, pomija w analizie pewne istotne punkty strukturalne, które zwyczajnie nie pasują do jego teorii. Obecność złotego podziału można zatem podważyć. Jednak słuchając utworu i podążając za jego dramaturgią wyczuwamy dobrze skonstruowaną formę, która daje poczucie porządku, symetrii, logiki. Nie bez powodu Muzyka uważana jest za arcydzieło klasyki XX wieku.
Ale spójrzmy też na kolejne przykłady, w których złote cięcie występuje w ważnych momentach formalnych: kulminacji, rozpoczęcia nowej części utworu lub powrotu tematu początkowego (często repryzy lub A’ w ABA’), istotnej zmiany muzycznej (harmonicznej, fakturalnej, dynamicznej), czy dojścia do kulminacji. Douglas Webster w artykule Golden-Mean Form in Music podaje utwory należące do kanonu muzyki minionych epok, w których analitycznie wykazał istnienie złotej proporcji.
Ludwig van Beethoven, Kwartet smyczkowy c-moll op. 18 nr 4 (0,618)
Jan Sebastian Bach, Preludium Fis-dur nr 13 BWV 882 (0,613)
Wolfgang Amadeus Mozart, Kwartet smyczkowy Es-dur KV 428 (0,616)
Fryderyk Chopin, Nokturn c-moll op. 48, nr 1 (0.618)
Arnold Schönberg, IV Kwartet smyczkowy op. 37, część III (0.611)
Hipoteza istnienia złotego podziału w utworach muzycznych jest dla niektórych muzykologów wątpliwa. Charles Madden uważa, że rezultaty badań nad obecnością złotej proporcji w utworach muzycznych są kontrowersyjne głównie dlatego, że opierają się na mało precyzyjnych obliczeniach: autorzy analiz pomijają na przykład introdukcje lub kody utworów, akceptują niedokładności wyliczeń, wskazując na obecność podziału jedynie zbliżonego do złotego cięcia, nie zaś samego w sobie. Dopiero współczesne, dokładniejsze badania dotyczące tego zjawiska zaczynają weryfikować wcześniejsze teorie. Sam Madden przyjmuje, że tolerowalnym zaokrągleniem liczby φ w muzyce jest 0,618. Jednak niektóre z przedstawionych utworów nie mieściłyby się już w tej kategorii. Zatem, czy idąc jego drogą myślenia nie powinniśmy dążyć do możliwie największej precyzji? Wówczas okazać się może, że złota proporcja właściwie nie jest obecna w żadnym z tych utworów. Pojawiają się pytania: czy w badaniach powinniśmy mierzyć odcinki czasu w sposób obiektywny (opierając się tylko na partyturze, długości nut i taktów), czy też subiektywny (biorąc pod uwagę wykonanie – a jeśli tak, to które?). Nawet jeśli uda się rozwiązać ten dylemat to pozostaje kolejny problem: liczba wyrażająca złotą proporcje w utworze nigdy (lub prawie nigdy) nie będzie tożsama z liczbą φ – która jest niewymierna.
Kto więc wygrywa w starciu między abstrakcyjnym modelem a namacalną rzeczywistością? Z jednej strony trudno jest przeprowadzić niebudzący sprzeciwu dowód na istnienie złotego podziału w muzyce – z drugiej równie trudno byłoby też temu istnieniu kategorycznie zaprzeczyć. Być może rozwiązanie leży gdzieś po środku. Złoty podział urzeczywistniając się w muzyce siłą rzeczy traci nieco ze swej „niewymiernej doskonałości” – ale tak to już jest z abstrakcyjnymi modelami. Nie mogą przystawać ściśle do naszej, ludzkiej rzeczywistości, dlatego że my sami – poznając świat przez zmysły – jesteśmy nieprecyzyjni. Mój stolik to około pół metra, ale miarka mówi, że bardziej 52 cm, i boję się nawet spytać, co tam się dzieje w mikroskali. Zaokrąglamy, przybliżamy, mierzymy coś na oko, coś się mniej więcej zasłyszy, odniesie jakieś wrażenie. I to jest naturalne, ludzkie.
Złotego podziału nie da się przenieść na grunt muzyki w sposób ścisły, w utworze będzie zawsze wypadał około 2/3 całości, lub raczej 3/5, 5/8, 8/13… Te ułamki pojawiają się tutaj nieprzypadkowo – zauważmy, że kolejne tworzące je liczby tworzą ciąg Fibonacciego, i posiadają tę niezwykłą własność, że stopniowo coraz lepiej przybliżają liczbę φ. Właśnie z tym zjawiskiem – przybliżaniem – mamy i będziemy mieć do czynienia w muzyce, ale i w życiu. Bo może nie o ścisłość tu chodzi, nie o zegarmistrzowską precyzję w wyliczaniu proporcji, w odmierzaniu długości taktów, kreśleniu pauz i podwójnych linii – ale o poczucie, że coś jest tak, jak powinno być. I jest piękne, nawet niedoskonałe. Nawet jeśli to tylko przybliżanie ideału.
Literatura:
- Charles Madden, Fractals in Music. Introductory Mathematics for Musical Analysis, High Art Press, 1999.
- Ernő Lendvaï, Béla Bartók. An analysis of his music, Kahn & Averill, 1979.
- J.H. Douglas Webster, Golden-Mean Form in Music, “Music & Letters”, 1950.
- Jonathan Kramer, The Fibonacci Series in Twentieth-Century Music, “Journal of Music Theory”, 1973.
- Matila C. Ghyka, Złota liczba. Rytuały i rytmy pitagorejskie w rozwoju cywilizacji zachodniej, Universitas, 2014.
- Tadeusz A. Zieliński, Bartók, PWM, 1980.
- Witold Rudziński, Warsztat kompozytorski Béli Bartóka, PWM, 1964.




